
Pandalism
Felix DMR's Blog
Programming, Electronics, Autonomous Vehicles and other interests!
Copyright © 2023 Pandalism
Approximating Pi using Monte Carlo Methods
20 September 2020
[
Lately been mostly using python, so to not let the knowledge of Matlab slip away I thought I should do minor exercises also in Matlab…In this case, I chose to approximate Pi using Monte Carlo methods, another quick 30min project!
Monte Carlo methods
Monte Carlo methods/simulations/experiments, are basically using randomly distributed samples to solve problems which otherwise might be quite difficult so solve using analytical means, like very complex multi-dimensional integrations, or to calculate overall uncertainty of a large number of small events with different probabilities. It’s used almost everywhere, examples:
- Calculate risk in finance and logistics
- Weather prediction
- Reliability and predictive maintenance
- Localisation and SLAM
- Animation and video game ray tracing (modelling a sample of photons as it bounces around the room)
- Rarified gas flows (where it can’t be modelled as a fluid and modelling each individual molecule is prohibitive)
- Almost anything actually.
It can get quite complicated in application but overall summary is throwing a lot of random sample points at a problem until you get a ‘rough picture of the solution’. This is usually easier than calculating the ‘accurate picture of the solution’ and at the same time it gives much better accuracy and granularity of outcomes as opposed to just following the boundaries such as ‘best-case scenarios’ and ‘worst-case scenarios’.
Finding Pi with Monte Carlo Simulation
I’ve happened to use Monte Carlo methods to help predict battery life in electric vehicles, but as usual in engineering you mostly use the tools instead of creating them, and I wanted to try it out… so I decided to do find Pi using Monte Carlo Simulation. I make no allusions here, it’s basically like writing ‘Hello World’ in the algorithm world.
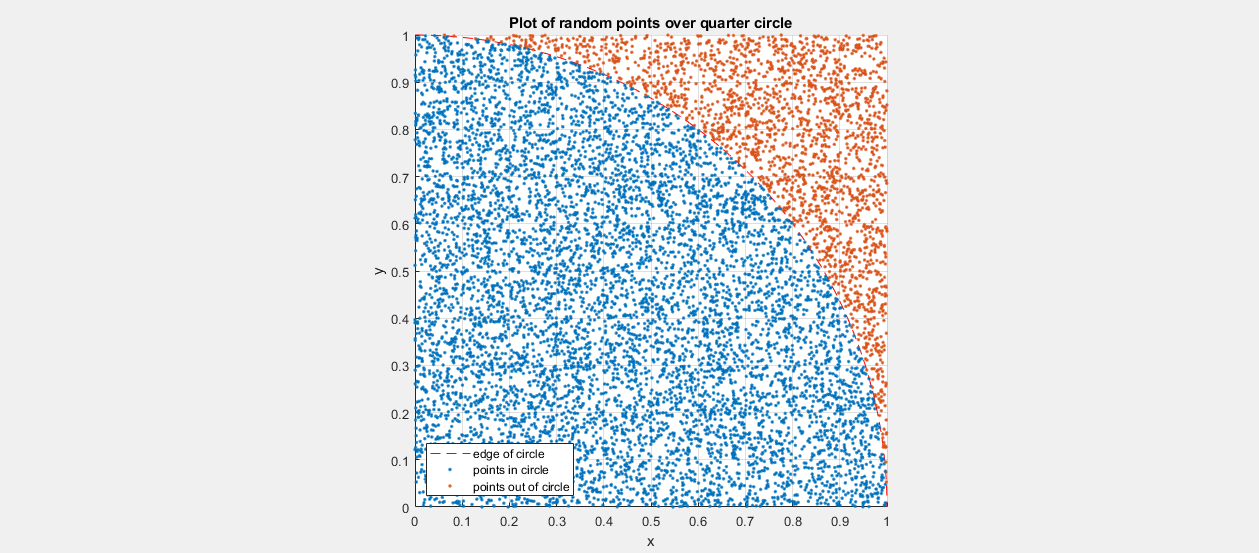
The logic is as follows: knowing the area of a perfect circle, radius r, and the area of a perfect square, length r, one can find Pi using the ratio of the areas.
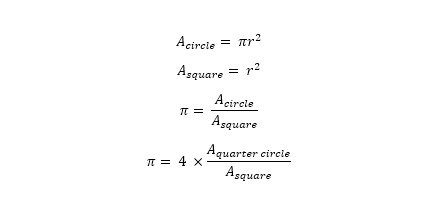 Not sure if this even requires an image but eh…
Not sure if this even requires an image but eh…
I find it much easier to think of it with a quarter of a circle (origin at [0,0]) within a square (with corners at [[0,0],[0,1],[1,1],[1,0]]). Then finding what’s inside the circle is just a simple sqrt(x^2 + y^2) < 1.
 What I mean by a quarter of a circle within a square
What I mean by a quarter of a circle within a square
So, imagining that we have no way to directly measure the area of either the circle or the square, Monte Carlo Methods allow us to indirectly measure them by throwing a uniformly distributed set of random points within the square, and seeing where they fall, whether its in the quarter circle or not. From that you can count the points and calculate Pi.
Since the samples are uniformly distributed across the whole area, the amount of points in each section will approximate the area of the section.
Now, its important to note that this is only approximately the area of that section due to the uniform distribution, but they are still samples and so they won’t be exact, the good news is that the more samples you throw at a problem the more accurate it should be… The terrible news is if your samples are not truly random or have inexact distribution, this whole concept breaks down.
Anyways enough silly write up, here is the Matlab script output:
Matlab script
There’s absolutely nothing fancy about the script but here it is if anyone wants to see it/replicate it in another language:
Conclusion
Nothing to really conclude here, its a fun little exercise, that’s all!
Links
- Marble Science has a great video on Monte Carlo Simulations, and not only that all his videos are done with a mix of python and blender to fantastic 3d simulation results, he really deserves more subscribers!

Copyright © 2023 Pandalism
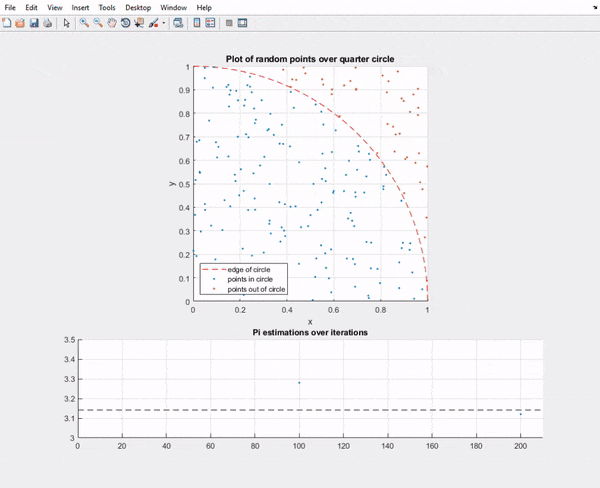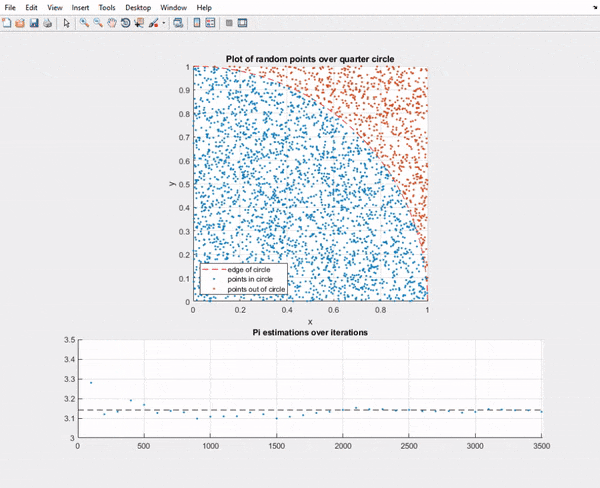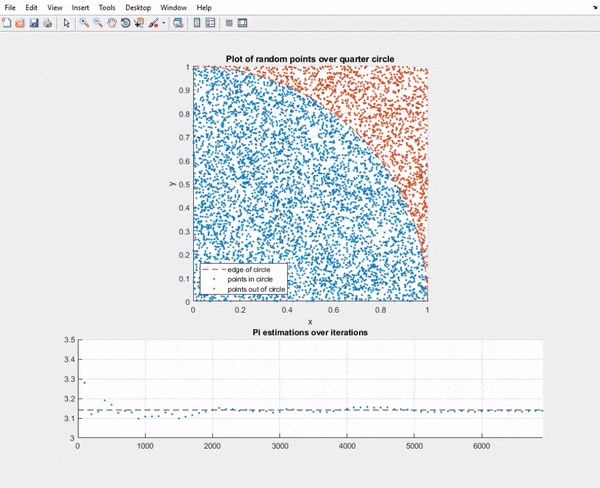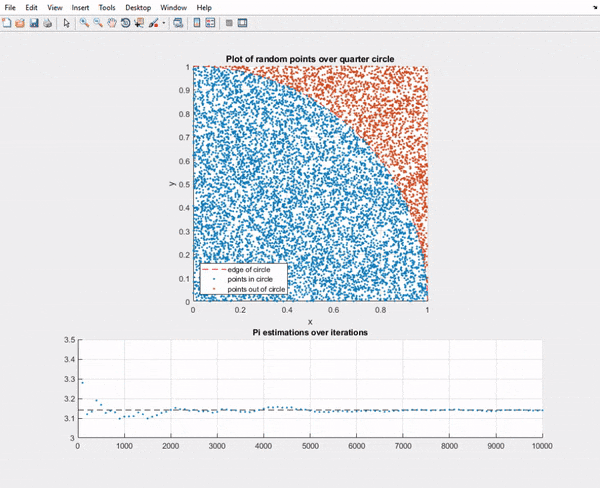 As you can see in the first batch of points the error of pi is higher and dances around it, but the longer it goes on the closer it gets.
As you can see in the first batch of points the error of pi is higher and dances around it, but the longer it goes on the closer it gets.